---

Background

In previous parts of my project, I built different n-gram models to predict the probability of each word in a given text. This probability is estimated using an n-gram — a sequence of words of length n — which contains the word. The below formula shows how the probability of the word “dream” is estimated as part of the trigram “have a dream”:

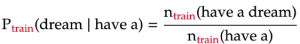
We train the n-gram models on the book “A Game of Thrones” by George R. R. Martin (called train). We then evaluate the models on two texts: “A Clash of Kings” by the same author (called dev1), and “Gone with the Wind” — a book from a completely different author, genre, and time (called dev2).

The metric to evaluate the language model is average log-likelihood: the average of the log probability that the model assigns to each word in the evaluation text.

Often, the log of base 2 is applied to each probability, as is the case in the first two parts of the project. Nevertheless, in this part, I will use a natural log, as it makes it simpler to derive the formulas that we will be using.

Problem

In part 2, the various n-gram models — from unigram to 5-gram — were evaluated on the evaluation texts (dev1 and dev2, see graphs below).

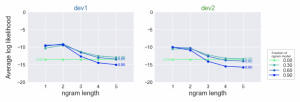
From this, we notice that:

• The Bigram model performs slightly better than the unigram model. This is because the previous word to the bigram can provide important context to predict the probability of the next word.
• Surprisingly, the trigram model and up is much worse than bigram or unigram models. This is largely due to the high number of trigrams, 4-grams, and 5-grams that appear in the evaluation texts but nowhere in the training text. Hence, their predicted probability is zero.
• For most n-gram models, their performance is slightly improved when we interpolate their predicted probabilities with the uniform model. This seems rather counter-intuitive since the uniform model simply assigns equal probability to every word. However, as explained in part 1, interpolating with this “dumb” model reduces the overfit and variance of the n-gram models, helping them generalize better to the evaluation texts.

In this part of the project, we can extend model interpolation even further: instead of separately combining each n-gram model with the uniform, we can interpolate different n-gram models with one another, along with the uniform model.

What to interpolate?

The first question to ask when interpolating multiple models together is:

Which n-gram models should we interpolate together to give the best result on the evaluation texts?

To answer this question, we use the simple strategy outlined below:

1. First, we start with the uniform model. This model will have very low average log-likelihoods on the evaluation texts since it assigns every word in the text the same probability.
2. Next, we interpolate this uniform model with the unigram model and re-evaluate it on the evaluation texts. We naively assume that the models will have equal contribution to the interpolated model. As a result, each model will have the same interpolation weight of 1/2.
3. We then add the bigram model to the mix. Similarly, in this 3-model interpolation, each model will simply have the same interpolation weight of 1/3.
4. We keep adding higher n-gram models to the mix while keeping the mixture weights the same across model, until we reach the 5-gram model. After each addition, the combined model will be evaluated against the two evaluation texts, dev1 and dev2.

Coding the interpolation

In part 2, each evaluation text had a corresponding probability matrix. This matrix has 6 columns — one for each model — and each row of the matrix represents the probability estimates of each word under the 6 models. However, since we want to optimize the model performance on both evaluation texts, we will vertically concatenate these probability matrices into one big evaluation probability matrix (803176 rows × 6 columns):