Contents
Introduction

Optimization shows up everywhere in machine learning, from the ubiquitous gradient descent to quadratic programming in SVM, to expectation-maximization algorithm in Gaussian mixture models.
However, one aspect of optimization that always puzzled me is duality: what on earth are a primal form and dual form of an optimization problem, and what good do they serve?
Therefore, in this project, I will:
- Go over the primal and dual forms for the most basic optimization problem: linear programming.
- Show that by solving one form of the optimization problem, we will have also solved the other one. This requires us to prove two fundamental duality theorems in linear programming: weak duality theorem and strong duality theorem. The former theorem will be proven in this part, while the latter will be proven in the next part of the project.
- Explain why we should care about duality by showing its application to some data science problems.
Linear programming
Definition
All (constrained) optimization problems have three components:
1.Objective function: the function whose value we are trying to optimize, which can mean minimize or maximize depending on the problem. The value of the objective function will be called the objective value from here on.
2.Decision variables: the variables in the objective function whose value will be fine-tuned to give the objective function its optimal value.
3.Constraints: additional equations or inequalities that the decision variables must conform to.
With these components, we can define linear programming as such:
Linear programming is an optimization problem where the objective function and constraints are all linear functions of the decision variables.
This principle can be seen in the following formulation of a linear program:
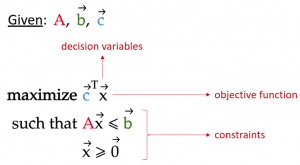
where
x: vector containing the decision variables
c: vector containing coefficients for each decision variable in the objective function. For simplicity, we will call these coefficients the objective coefficients from here on.
A: matrix in which each row contains the coefficients of each constraint
b: vector containing the limiting values of each constraint
Note that the vector inequalities in the above formula imply element-wise inequalities. For example, x ≥ 0 means every element of x must be greater or equal to zero.
Geometric interpretation of a linear program
Although the above formula of a linear program seems quite abstract, let’s see what it looks like using a simple example.
- Suppose we have only had 2 decision variables, x₁, and x₂. Therefore, our vector
xis simply [x₁, x₂]
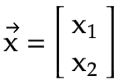
For More Detail, Please check the Link
Hiring Data Scientist / Engineer
We are looking for Data Scientist and Engineer.
Please check our Career Page.
Data Science Blog
Please check our other Data Science Blog
AI / Data Science Project
Please check about experiences for Data Science Project
Vietnam AI / Data Science Lab

Please also visit Vietnam AI Lab