Contents
Definition
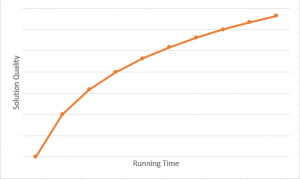
In computer science, most algorithms run to completion: they provide a single answer after performing some fixed amount of computation. But nowadays, in machine learning generation, the models take a long time to train and predict the result, the user may wish to terminate the algorithm before completion. That’s where anytime algorithm came in, an algorithm that can return a valid solution even if it is interrupted before it ends. The longer it keeps running, the better solution the user gets.
What makes anytime algorithms unique is their ability to return many possible outcomes for any given input. An anytime algorithm uses many well-defined quality measures to monitor progress in problem-solving and distributed computing resources. While this may sound like dynamic programming, the difference is that it is fine-tuned through random adjustments, rather than sequential.
Algorithm prerequisites
Initialize: While some algorithms start with immediate guesses, anytime algorithm take more calculated approach and have a start–up period before making any guesses
Growth direction: How the quality of the program’s “output” or result, varies as run time
Growth rate: Amount of increase with each step. Does it change constantly or unpredictably?
End condition: The amount of runtime needed
Case studies
-
Clustering with time series
In clustering, we must compute distance or similarity between pairs of time series and we also have a lot of measurements. As many types of research proved that dynamic time warping (DTW) is more robust than others, but the complexity O(N2) of DTW makes computation more trouble.
With anytime algorithm, the life is easier than ever. Below is pseudocode for anytime clustering algorithm.
Algorithm [Clusters] = AnytimeClustering(Dataset)
1. aDTW = BuildApproDistMatrix(Dataset)
2. Clusters = Clustering(aDTW, Dataset)
3. Disp("Setup is done, interruption is possible")
4. O = OrderToUpdateDTW(Dataset)
5. For i = 1:Length(O)
6. aDTW(O(i)) = DTW(Dataset, O(i))
7. if UserInterruptIsTrue()
8. Clusters = Clustering(aDTW, Dataset)
9. if UserTerminateIsTrue()
10. return
11. endif
12. endif
13. endfor
14. Clusters = Clustering(aDTW, Dataset)
Firstly, we need to approximate the distance matrix of the dataset.
Secondly, we do cluster to get the very basic result.
Thirdly, we make some heuristic to find the optimal solution to update the distance matrix, after each updating, we get a better result than before.
Lastly, if the algorithm keeps running longer, it will finish the task and we can get the final optimal output.
-
Learning optimal Bayesian networks
Another common example for anytime algorithm is searching optimal output in Bayesian networks. As we know that Bayesian network is NP–hard. If we have too many variables or events, the algorithm will fail due to limited time and memory. That’s why the anytime weighted A* algorithm is often applied to find an optimal result.
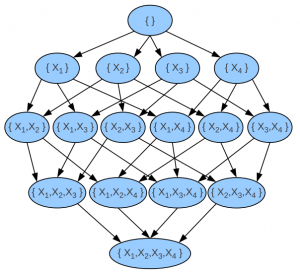
Weighted A* algorithm use this cost function to minimize
f(n) = g(n) + ε * h(n)
where n is the last node on the graph, g(n) is the cost of the path from the start node to n, and h(n) is a heuristic that estimates the cost of the cheapest path from n to the last node, ε gradually lowers to 1. The anytime algorithm bases on this cost function to stop and continue at any time.