Contents
Background
In part 1 of my project, I built a unigram language model: it estimates the probability of each word in a text simply based on the fraction of times the word appears in that text.
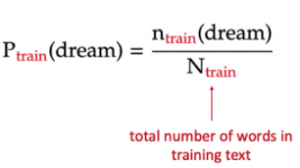
The text used to train the unigram model is the book “A Game of Thrones” by George R. R. Martin (called train). The texts on which the model is evaluated are “A Clash of Kings” by the same author (called dev1), and “Gone with the Wind” — a book from a completely different author, genre, and time (called dev2).

In this part of the project, I will build higher n-gram models, from bigram (n=2) to 5-gram (n=5). These models are different from the unigram model in part 1, as the context of earlier words is taken into account when estimating the probability of a word.
Higher n-gram language models
Training the model
For a given n-gram model:
- The probability of each word depends on the n-1 words before it. For a trigram model (n = 3), for example, each word’s probability depends on the 2 words immediately before it.
- This probability is estimated as the fraction of times this n-gram appears among all the previous (n-1)-grams in the training set. In other words, training the n-gram model is nothing but calculating these conditional probabilities from the training text.
The example below shows how to calculate the probability of a word in a trigram model:
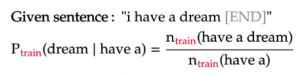
Dealing with words near the start of a sentence
In higher n-gram language models, the word near the start of each sentence will not have a long enough context to apply the formula above. To make the formula consistent for those cases, we will pad these n-grams with sentence-starting symbols [S]. Below are two such examples under the trigram model:
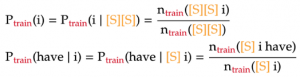
From the above formulas, we see that the n-grams containing the starting symbols are just like any other n-gram. The only difference is that we count them only when they are at the start of a sentence. Lastly, the count of n-grams containing only [S] symbols is naturally the number of sentences in our training text:
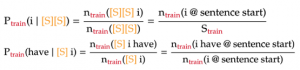
Dealing with unknown n-grams
Similar to the unigram model, the higher n-gram models will encounter n-grams in the evaluation text that never appeared in the training text. This can be solved by adding pseudo-counts to the n-grams in the numerator and/or denominator of the probability formula a.k.a. Laplace smoothing. However, as outlined in part 1 of the project, Laplace smoothing is nothing but interpolating the n-gram model with a uniform model, the latter model assigns all n-grams the same probability:
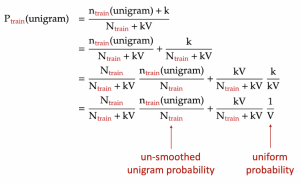
Hence, for simplicity, for an n-gram that appears in the evaluation text but not the training text, we just assign zero probability to that n-gram. Later, we will smooth it with the uniform probability.