Contents
In this post, I will explain how to calculate a Bayesian estimator. The taken example is very simple: estimate the parameter θ of a Bernoulli distribution.
A random variable X which has the Bernoulli distribution is defined as
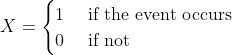
with
![]()
In this case, we can write
![]() .
.
In reality, the simplest way to estimate θ is to sample X, count how many times the event occurs, then estimate the probability of occurring events. This is exactly what the frequentists do.
In this post, I will show how do the Bayesian statisticians estimate θ. Although this doesn’t have a meaningful application, it helps to understand how do Bayesian statistics work. Let’s start.
The posterior distribution of θ
Denote Y as the observation of the event. Given the parameter θ, if we sample the event n time, then the probability that the event occurs k time is (this is called the probability density function of Bernoulli )
![]()
In Bayesian statistics, we would like to calculate
By using the Bayesian formula, we have
With the prior distribution of theta as a Uniform distribution, p(θ) = 1, and it is easy to prove that
where Γ is the Gamma distribution. Hence, the posterior distribution is
Fortunately, this is the density function of the Beta distribution:
We use the following properties for evaluating the posterior mean and variance of theta.
If , then
Simulation
In summary, the Bayesian estimator of theta is the Beta distribution with the mean and variance as above. Here are the Python codes for simulating data and estimating theta
def bayes_estimator_bernoulli(data, a_prior=1, b_prior=1, alpha=0.05):
'''Input:
data is a numpy array with binary value, which has the distribution B(1,theta) a_prior, b_prior: parameters of prior distribution Beta(a_prior, b_prior) alpha: significant level of the posterior confidence interval for parameter Model:
for estimating the parameter theta of a Bernoulli distribution the prior distribution for theta is Beta(1,1)=Uniform[0,1] Output:
a,b: two parameters of the posterior distribution Beta(a,b)
pos_mean: posterior estimation for the mean of theta
pos_var: posterior estimation for the var of theta'''
n = len(data)
k = sum(data)
a = k+1
b = n-k+1
pos_mean = 1.*a/(a+b)
pos_var = 1.*(a*b)/((a+b+1)*(a+b)**2)
## Posterior Confidence Interval
theta_inf, theta_sup = beta.interval(1-alpha,a,b)
print('Prior distribution: Beta(%3d, %3d)' %(a_prior,b_prior))
print('Number of trials: %d, number of successes: %d' %(n,k))
print('Posterior distribution: Beta(%3d,%3d)' %(a,b))
print('Posterior mean: %5.4f' %pos_mean)
print('Posterior variance: %5.8f' %pos_var)
print('Posterior std: %5.8f' %(np.sqrt(pos_var)))
print('Posterior Confidence Interval (%2.2f): [%5.4f, %5.4f]' %(1-alpha, theta_inf, theta_sup))
return a, b, pos_mean, pos_var
# Example
n = 129 # sample size
data = np.random.binomial(size=n, n=1, p=0.6)
a, b, pos_mean, pos_var = bayes_estimator_bernoulli(data)
And the result is
Hiring Data Scientist / Engineer
We are looking for Data Scientist and Engineer.
Please check our Career Page.
Data Science Project
Please check about experiences for Data Science Project
Vietnam AI / Data Science Lab
Please also visit Vietnam AI Lab
