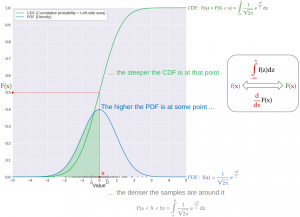
• The cumulative probability at some value x is the probability that the random variable X has a value that is lower than x: P(X < x). This can be obtained by integrating the probability density function (PDF)* of X from negative infinity to x. Geometrically, this is the area under the PDF to the left of x, which I will call the “left-side area” from here on (see the green area in the graph below).
• As a result, for any value of x, we can always calculate its cumulative probability / left-side area. The function that converts the value x into its cumulative probability is appropriately called the cumulative distribution function (CDF)*. In the below graph for Gaussian distribution, the left-side area at x=0 is of course 0.5; alternatively, we can infer this area by looking at the CDF at x=0, which also comes out to be 0.5 (see the red points).

* Technically, PDF, and CDF are functions that transform one variable to another, while density and cumulative probability are outputs of these functions respectively. However, the word PDF is often used interchangeably with density and CDF with cumulative probability.